量子コンピュータが徐々に実用化が見えてきています。とは言っても私たちの家庭のPCが量子コンピュータになることはありません。特殊で量子コンピュータが得意な計算をサーバに送って、結果をもらうという使い方になります。なので、現在、私たちが使っている古典コンピュータがなくなることはありません。

　量子コンピュータをできるだけ簡単に説明して、qiskitというpythonのライブラリで遊んでみるところまで解説してみたいと思います。

量子ビットの仕組み

量子コンピュータのビットは、私たちが使っている古典コンピュータのビットとはかなり違う仕組みをしています。古典コンピュータのビットは、ある素子の電圧がONかOFFかで、そのビットの値が0か1かを決めています。量子コンピュータのビットも、ある量子の状態を観測してビットの0と1を判定するのですが、この量子は観測するまで状態が確定しません。0か1かどっちかわからない状態で計算をして最後に観測したら結果だけわかるという使い方になります。

ただ、量子ビットを操作することによって、0の確率を高くしたり、1の確率を高くすることはできます。量子ビットを理解する上で大事なブロッホ球の図を書きます。

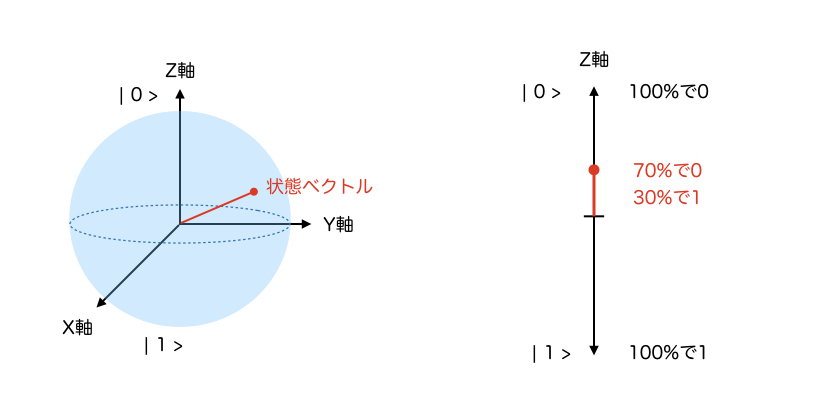
左側は、XYZ軸を持つ空間上に量子の状態を表す球面を描き、その球面上に量子の状態があるとしています。ビットの値を決めるのはZ軸です。Z軸上のてっぺんがビット0に、反対側の真下がビット　1になる状態です。その他の球面上の点は、Z軸に射影して上の方であれば0の確率が高い、下の方であれば1の確率が高くなりますが、上で記述したように観測するまでどっちになるかわわかりません。赤線の状態ベクトルの例だと、70%ぐらいの確率で0、30%の確率で1という状態になります。

このブロッホ球は、数学的に解釈するためのもので、実際には電子のスピンの向きを使っていたりしますが、総じて観測するまでわからないものを使っています。

このわからないまま計算を実行できることが、並列に計算できる仕組みでもあり、量子コンピュータの独特な特徴でもあります。計算とは何かというと、このブロッホ球的に言うと、ある量子の状態をX軸を中心に回転させたり、Y軸中心に回転させたり、はたまた任意の軸を作ってその軸で回転させたりと、それによって状態が変わり、0の確率、1の確率も変わっていきます。ある量子の状態に基づいて別の量子を操作することもできます。

量子回路

では、この量子ビットを使って、簡単なビットの足し算を演算する量子回路を書いてみます。

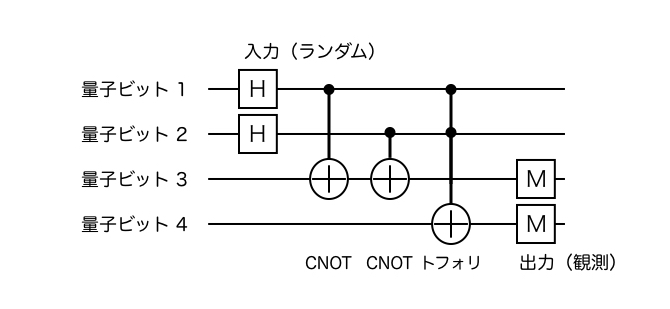
量子ビットを4つ使います。量子ビット１と２は入力ビットで、量子ビット３と４は出力ビットとします。

全ての量子ビットは0で初期化されているとします。まず、量子ビット1と2に「H」というアダマールゲートを使い、0が50％、1が50%という状態にします。つまり完全ランダムなビットとなります。

次にCNOTゲート（制御ビットが1の時だけ標的ビットを反転させる）を使い、量子ビット3に足し算結果の下位ビットをだすようにします。そして、量子ビット４にトフォリゲート（制御ビット2つが両方1の時だけ標的ビットを反転させる）を使うことで、足し算の繰り上がりビットをだすようにします。

最後に量子ビット3と4を「M」で観測しています。観測した時点で量子ビット3と4のビットが決まります。入力は「H」でランダムになっているので結果は観測するまでわかりませんが、00か01か10になるはずです。いわゆる全ての入力パターンを同時に計算しているイメージです。これが量子コンピュータの特徴です。結果はやる度に変わりますが、その確率分布を見るとどの結果が一番あり得るのか等がわかってきます。

qiskitで量子回路を組んでみる

qiskitはIBM Researchによって開発された量子コンピュータ用のフレームワークで、python用のライブラリもあります。まずは、pythonのqiskitをインストールします。

# pip install qiskit

次に、上で説明した足し算の量子回路をpythonコードで書きます。

from qiskit import *

def main():

    # シミュレータの初期化
    simulator = Aer.get_backend('qasm_simulator')
    # 量子回路の作成
    circuit = QuantumCircuit(4,2)
    # 0ビット目と1ビット目をアダマールゲートで、0が50%、1が50%の状態にする
    circuit.h(0)
    circuit.h(1)
    # CNOTゲート
    circuit.cx(0,2)
    circuit.cx(1,2)
    # トフォリゲート
    circuit.ccx(0,1,3)
    # 2ビット目、3ビット目を観測する
    circuit.measure([2,3], range(2))
    # 回路の表示
    print(circuit)
    # 実行
    job = execute(circuit, simulator, shots=1000)
    result = job.result()
    count = result.get_counts(circuit)
    # 結果表示
    print(count)

if __name__ == '__main__':
    main()

このスクリプトを実行すれば、シミュレータ相手ですが、作成した量子回路の演算をしてくれます。1000回実行した時の結果の分布を表示するようにしています。

        ┌───┐                     
q_0: |0>┤ H ├──■─────────■────────
        ├───┤  │         │        
q_1: |0>┤ H ├──┼────■────■────────
        └───┘┌─┴─┐┌─┴─┐  │  ┌─┐   
q_2: |0>─────┤ X ├┤ X ├──┼──┤M├───
             └───┘└───┘┌─┴─┐└╥┘┌─┐
q_3: |0>───────────────┤ X ├─╫─┤M├
                       └───┘ ║ └╥┘
 c_0: 0 ═════════════════════╩══╬═
                                ║ 
 c_1: 0 ════════════════════════╩═
                                  
{'10': 248, '01': 513, '00': 239}

コンソール画面にこのように表示されました。最後の行が結果のカウント数です。 10が248回、01が513回、00が239回です。 01は、1+0でも0+1でも01になるため、2倍の確率になっています。ランダムに2ビット選んだ足し算の結果の確率分布に合ってますね。

量子コンピュータの応用

足し算だけでは、量子コンピュータのありがたみが全くわからないと思いますが、いろいろな状態の計算を並列にできることが、複雑な問題ではありがたい場合があります。

例えば、データベース検索の例だと、膨大なデータの中からあるデータを見つけるためには、O(n)の計算量がかかると思われますが、グローバーの探索アルゴリズムというのを使うと、量子コンピュータでO(√n)で探索できると言われています。

また、現在の暗号技術のベースとなっている素因数分解の問題についてもショアのアルゴリズムを使うと高速に解けるというものです。量子ビットがかなり必要なのでまだ現実的に暗号解読はできないです。

今後、量子コンピュータのハードウェア技術が進歩することによって、このような複雑な問題をAPIでサーバの量子コンピュータに投げて短時間で結果をもらうという世界がはじまりそうです。